Roundabouts inside Roundabouts and Perspective-ception

Author’s Note

This post was originally writted for academic credit in the course ISCI 1A24 at McMaster University. The original is behind a class login at Synopsis Beta, but this version is entirely unedited. Please forgive the roughness of the post, this was years ago. I’m leaving this here only for posterity (and to flesh out my website).

Article

Would you believe me if I tell you that there exists five small roundabouts surrounding a large roundabout rotating in the opposite direction? The commonly-called “magic roundabout” was first installed in Swindon, UK, and, while seemingly insane, it actually does work (See Figure 1) (Marshall, 2014).

They were designed to work without requiring additional knowledge of handling the junction by exploiting the simple rules that drivers already know (Scott, 2015). This phenomenon is known as emergence – where large patterns result from the interaction of smaller entities, each following a set of simple rules (Wood and Ackland, 2007; Green, 1993). Individual behaviours are simple and predictable, but en masse, act completely differently[1].

Figure 1: The magic roundabout at Swindon, UK (BBC 2012)

The classic example is bird flocking behaviours, as shown by Reynolds’s boids simulation (Reynolds, 2001). Individually, they follow simple rules formed by years of evolution: avoid hitting others (separation), follow the movement of surrounding birds (alignment), and avoid becoming alone and falling to a predator (cohesion). Although these three rules are relatively simple, they are able to create a near-unpredictable organic mass when scaled up to hundreds or thousands of individuals. The individual does not intend to form this cloud, nor is there a leader organizing it, but the flock emerges nonetheless (See Figure 2).

Figure 2: Boids simulation demonstrating emergent flocking even without explicit programming for it (Softology, 2011)

This swarming behaviour can be found in many animals across nature, from fish to bison to even humans (Green, 1993). This is not immediately evident becuase we normally take an individual’s point of view. When an overarching perspective is taken, however, one can see that we organize ourselves into cities according to the same principles, and even travel in similar ways.

Emergence is not limited to physical behaviours either, as they can be seen in more theoretical circumstances. The stock market and the internet[2] both have no central “mind” but produce emergent systems simply based on the interactions of many smaller entities. It is of major interest in mathematics, where various forms of emergence are modelled (Langton, 1990), such as the cellular automaton like Conway’s Game of Life (Gardner, 1970). A closely related concept is the chaos game, where a fractal emerges from repeatedly choosing between a set of points and moving a fraction of the distance towards it[3] (See Figure 3) (Barnsley and Vince, 2010).

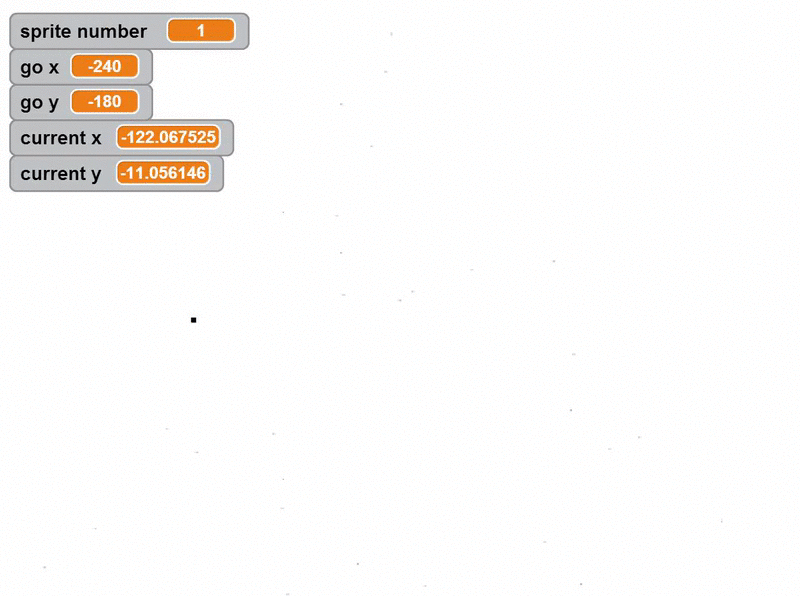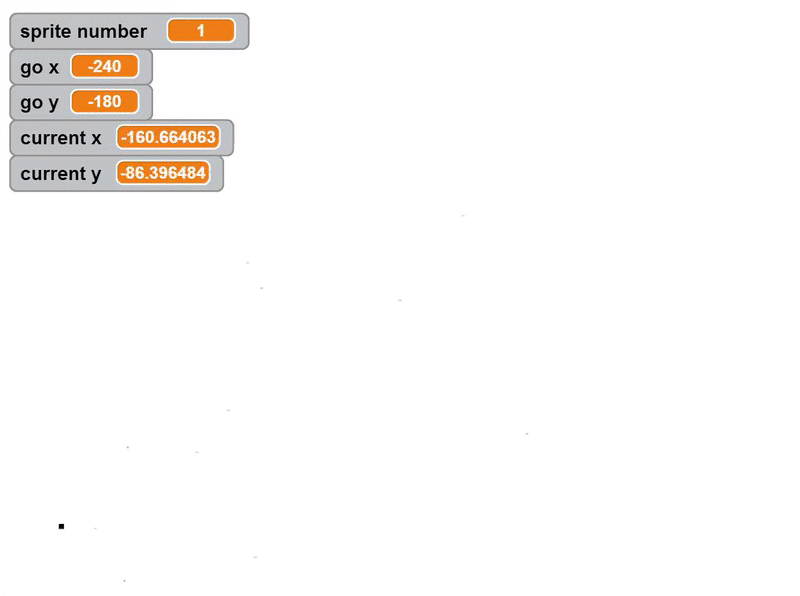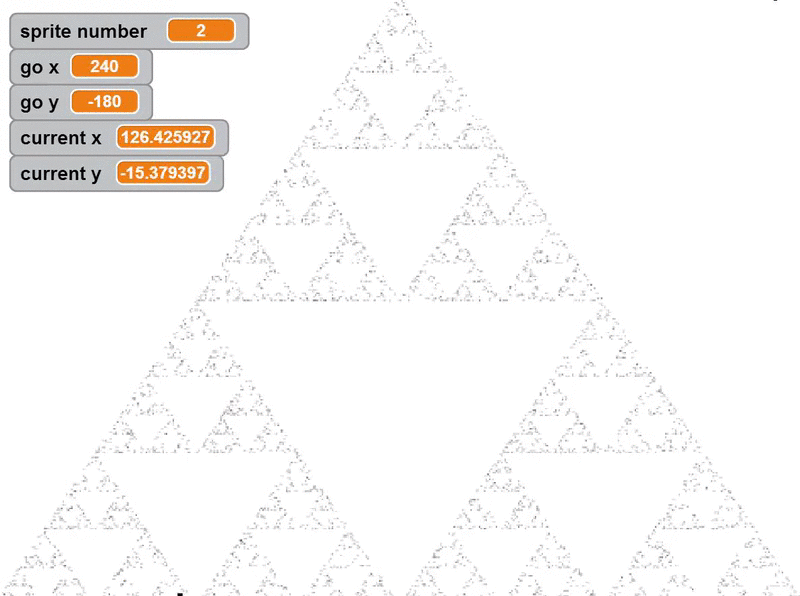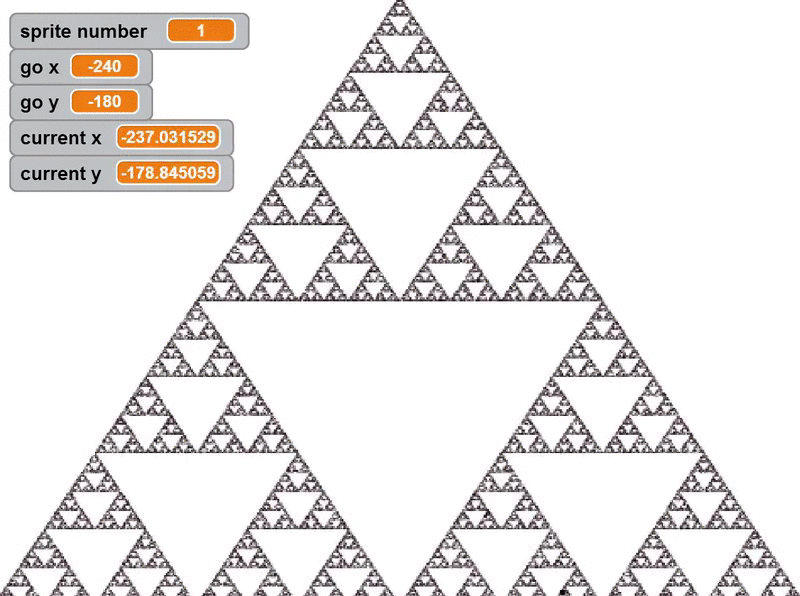
Figure 3: A sierpenski triangle constructed using a chaos game (Panuelos, J. 2013)

While being an interesting phenomenon, emergence also has practical applications. As shown before, weaker emergent patterns are used to organize and manipulate traffic, while reducing overhead knowledge to drivers. Additionally, emergence is used in solving and understanding complex systems that cannot be handled traditionally, such as the interactions of millions of cells (Green, 1993). This is the true strength of the study of emergence – it allows for the understanding of multiple scales at once, both what is happening to the individual and to the whole. In reality, our universe is built on emergence – biology is emergent of chemical reactions which are emergent of subatomic physics. Scale up, and ecology is emergent of individual organisms. Emergence allows for the understanding of the relationships between all these, creating a heuristic perspective of perspectives.

Asides

[1] Truthfully, the Swindon Magic Roundabout is a bit of a stretch in terms of emergence. Because it is so easy to predict and there is relatively little interactions between individuals, it exhibits very weak emergence.

[2] A personal favourite of mine is the open-source movement, where individuals spew small bits of code, useless on their own, into a central database. Somehow, this all comes together to create programs that can rival commercial ones, such as libreOffice to MSOffice, GIMP to Photoshop, and Linux distros to Windows/OS X.

[3] An example of a chaos game is take three points to form an equilateral triangle plus a random starting point, randomly choose one of the three, then draw a point halfway between the current point and the chosen point. Repeat this indefinitely, and you form a Sierpenski Triangle.

This can be seen in some code I wrote: http://scratch.mit.edu/projects/3229598/, or in python (just copy paste into any python IDE and it should work as long as you have the right libraries):

import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np

x=0
y=0
x2=0
y2=0
xar=[]
yar=[]
foo=0

fig=plt.figure()
ax1=fig.add_subplot(111)

def animate(i):
global x,y,x2,y2,foo
foo=np.random.randint(1,4)
if foo==1:
x2=-240
y2=-180
if foo==2:
x2=240
y2=-180
if foo==3:
x2=0
y2=180
x=((x+x2)/2)
y=((y+y2)/2)
xar.append(x)
yar.append(y)
ax1.clear()
ax1.scatter(xar,yar)

ani=animation.FuncAnimation(fig,animate)
plt.show()

References