Maτhematics has No Double τ
Author’s Note
This post was originally writted for academic credit in the course ISCI 1A24 at McMaster University. The original is behind a class login at Synopsis Beta, but this version is entirely unedited. Please forgive the roughness of the post, this was years ago. I’m leaving this here only for posterity (and to flesh out my website).
Article
03/14/15 – the most important Pi Day in a century has now come and gone, leaving mathematicians feeling about the same as everyone else is after St. Patrick’s Day. This is, of course, barring the fact that only Americans really use the MM/DD/YY system, and that it only works if the first two digits of the year is dropped. Add in the idea that the human construct of time is completely arbitrary, and one can see why the observance of Pi Day is questionable. Faulting a festival for being set at an arbitrary date, however, is not a very well-founded argument, as all festivals are arbitrary by nature. What is at fault here is not the day, but pi itself.
Pi as a number, is not wrong, of course. The circumference of any circle divided by its diameter will always be 3.1415…, and it has all the properties mathematics credits it with. It is irrational and transcendental, but then again, practically all numbers are (Arndt and Haenel, 2001; Bourbaki, 1998). Its usage as the primary circle constant present in mathematics, science, and engineering is, as stated by Michael Hartl in the Tau Manifesto, “confusing and unnatural” (Hartl, 2013). This largely stems from the discrepancy of pi’s ratio being circumference:diameter, despite circles being defined by points a radius distance from a centre.
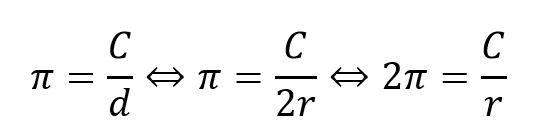
Figure 1: The factor of 2 inherent in the usage of pi=3.1415
This single difference creates a factor of 2 to appear whenever pi is used (see Fig 1). Pull up any physics formula sheet and you will likely find \(2π\) and \(4π^2\) half a dozen times. A number of mathematicians have suggested the usage of \(τ=2π\) to simplify these into \(τ\) and \(τ^2\). (Hartl, 2013; Abbott, 2012; Palais, 2009). This would also make trigonometry more sensible – \(1τ\) radian would be a single rotation, \(½τ\) would be half, \(¼τ\) would be a quarter and so on. This means that \(\sin(¼τ)\) would mean what it is meant to – the y-value of a quarter turn about the unit circle. Again, notice that the unit circle has a radius of 1, not diameter.
Common counterarguments include the area of a circle formula and Euler’s identity. Proving tau’s place in the latter is fairly easy; simply work from Euler’s formula and substitute \(τ\) for \(Θ\) (see Fig 2):
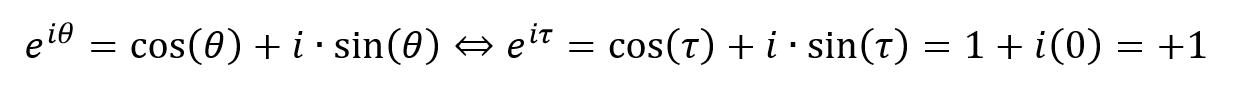
Figure 2: The mathematical beauty in using tau in Euler’s Formula
As for the area of the circle, yes it will become \(A=½τr^2\), but this reflects area as representative of an integral (see Fig 3):
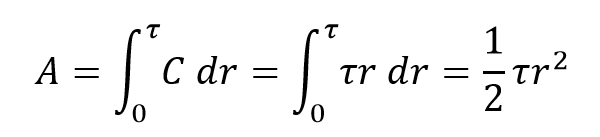
Figure 3: The area of a disk is the integral of the area of infinitely thin, concentric rings
This matches with any quadratic form formula resulting from an integral. Archimedes recognized this formula, equating the area of a disk with that of a triangle of base \(C\) and height \(r\) (Heath, 1931).
Majority of the reasons supporting the use of pi are historic. The usage of the symbol pi was popularized by Euler, which may have been the last time that the definition could be easily changed (Arndt and Haenel, 2001). Now that pi is firmly set in mathematics, the transition to tau as the true circle constant is much more difficult. The problem not so much for established mathematicians – those who would like to use tau can simply make a Let τ=2π statement. It is for the understanding of those learning math that tau is important, as it reveals much more of what the equations mean than pi does.
References
Abbott, S., 2012. Aftermath: My Conversion to Tauism. Math Horizons, [online] 19(4), pp.34–34. Available at: http://www.researchgate.net/publication/259735459_Aftermath_My_Conversion_to_Tauism [Accessed 18 Mar. 2015].
Arndt, J. and Haenel, C., 2001. Pi – Unleashed. [online] Springer Science & Business Media, p.270. Available at: http://books.google.com/books?id=QwwcmweJCDQC&pgis=1 [Accessed 18 Mar. 2015].
Bourbaki, N., 1998. Elements of the History of Mathematics. [online] Springer Science & Business Media, p.301. Available at: https://books.google.com/books?id=Qvo8-KC__VAC&pgis=1 [Accessed 18 Mar. 2015].
Hartl, M., 2013. The Tau Manifesto. [online] Available at: http://www.tauday.com/tau-manifesto [Accessed 18 Mar. 2015].
Heath, S.T.L., 1931. A Manual of Greek Mathematics. [online] Courier Corporation, p.552. Available at: http://books.google.com/books?id=_HZNr_mGFzQC&pgis=1 [Accessed 18 Mar. 2015].
Palais, R., 2009. π is wrong! The Mathematical Intelligencer, [online] 23(3), pp.7–8. Available at: http://link.springer.com/10.1007/BF03026846 [Accessed 18 Mar. 2015].