Does Dark Energy Actually Exist?

Author’s Note

This post was originally writted for academic credit in the course ISCI 3A12 at McMaster University. The original is behind a class login at Synopsis Beta, but this version is entirely unedited. Please forgive the roughness of the post, this was years ago. I’m leaving this here only for posterity (and to flesh out my website).

Article

Despite being an integral part of the standard model of cosmology in the last twenty years, dark energy may not actually exist according to a recently published paper that statistically demonstrates that observational data is consistent with a Universe without dark energy (Nielsen, Guffanti and Sarkar, 2016).

In 2011, three scientists – Saul Perlmutter, Brian Schmidt, and Adam Riess – were awarded the Nobel Prize in Physics for their work in the late 90s on the discovery of the acceleration in the expansion of the Universe (The Nobel Foundation, 2014). They had done this by looking at standard candles, particularly type Ia supernovae, which have very predictable magnitudes dependent on their distance (Riess et al., 1998; Perlmutter et al., 1999). This had been contrary to the expected result – that expansion should be decelerating due to the attracting force of gravity – and thus suggested that there has to be a constant outward pressure present in the vacuum to counteract gravity (Liddle, 2015). This pressure had previously been predicted, but later retracted, by Einstein as the cosmological constant, Λ – a fudge factor used to balance out gravity to give a static universe (Goldsmith, 1997). The same Λ can be interpreted as the dark energy, giving rise to the Λ-CDM model which, following Perlmutter, Schmidt, and Riess’ discovery, was widely adopted and became the standard model of cosmology (Liddle, 2015).

This theory is now under challenge by the aforementioned paper, claiming that the observational data gathered since Perlmutter, Schmidt, and Riess’ analysis fits a non-accelerating expansion scheme, and therefore a Universe without dark energy. They had used the same observational data, Type Ia supernovae, but a larger dataset – 740 – compared to Perlmutter’s 49 and Schmidt and Riess’ 10. Despite this larger set, however, they only achieved a 3σ confidence, equivalent to p<0.003, when the standard is 5σ, equivalent to p<3e-7, which is the same confidence found by Perlmutter, Schmidt, and Riess (Nielsen, Guffanti and Sarkar, 2016; Perlmutter et al., 1999; Riess et al., 1998). Thus, looking at the supernova data alone, none of the papers can conclusively prove the existence, or non-existence, of dark energy.

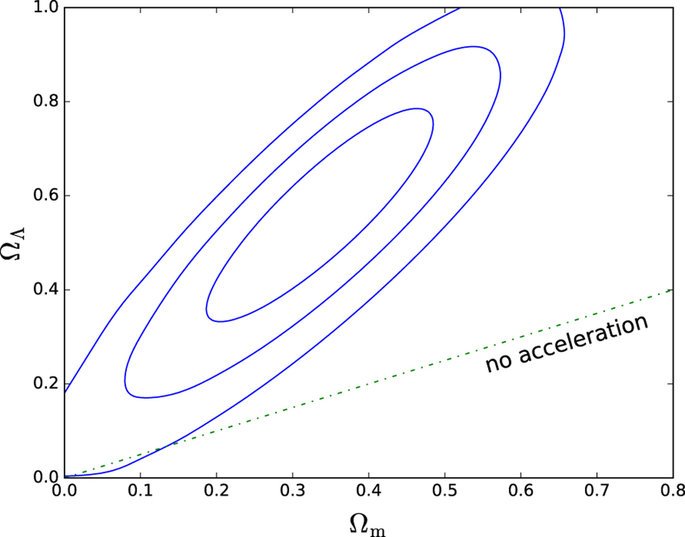
Figure 1: A contour plot of the confidence intervals on the Ωm-ΩΛ phase plane. Ωm is the density of dark matter divided by the Universe’s critical density – the density at which its topology is flat – while ΩΛ is the density of dark energy. The blue lines represent contours of 1σ, 2σ, and 3σ confidence from the inside out. Note that the 3σ contour crosses ΩΛ=0.0, indicating a possibility of nonexistent dark energy (Nielsen, Guffanti and Sarkar, 2016).

The original papers were able to achieve a 5σ confidence by interpreting the supernova data along with other observational data – in particular, the existence of dark matter (Perlmutter et al., 1999; Riess et al., 1998). Figure 1 shows a phase plot of Ωm vs ΩΛ, which represents the amounts of dark matter and dark energy respectively, with the 1σ, 2σ, and 3σ contours outlined in blue from smallest to largest (Nielsen, Guffanti and Sarkar, 2016). Take note that the contours show that a low to nonexistent amount of dark energy also represents a low amount of dark matter. However, dark matter is known to comprise a significant portion of the universe, 26.8%, and thus, ΩΛ must necessarily be higher than 0.2, eliminating the possibility of nonexistent dark energy (Ade et al., 2015).

Thus, the current standard theory of cosmology stands, continuing to prove true against criticism and remain the most accurate theory compared to observational data.

References