Tic-Tac-Torus
Author’s Note
This post was originally writted for academic credit in the course ISCI 3A12 at McMaster University. The original is behind a class login at Synopsis Beta, but this version is entirely unedited. Please forgive the roughness of the post, this was years ago. I’m leaving this here only for posterity (and to flesh out my website).
Article
A couple weeks ago by happenstance, I had come across a website: http://www.geometrygames.org/, by mathematician and cosmologist Jeff Weeks, which features familiar games involving topology (Weeks, 2017). Instead of the usual 2-dimensional flat boards, one can play chess, go, and tic-tac-toe on other spaces such as a torus and Klein bottle. With this, suddenly, the simple game of tic-tac-toe becomes much more interesting.
Take the usual 3×3 tic-tac-toe board. Mathematically, we call this board bounded, as nothing relevant exists past the top, bottom, left, and right edges. Suppose the left edge was glued to the right at the same orientation (Figure 1). Orientation simply means the direction in which the edges are glued together. Suppose the board was numbered according to a calculator – connecting the edges in the same orientation simply means connecting the squares 1,4,7 to 3,6,9 in that order, creating a cylinder, while opposing orientations means connecting 1,4,7 to 9,6,3 in that order, creating a Möbius strip.

Figure 1: A usual tic-tac-toe board, but with arrows showing the sides and orientation to attach them to form a cylinder. Adapted from (Weeks, 2017).
This creates a tic-tac-toe cylinder (Kinsey, 1993), and adds four new win conditions for either player – see for yourself by drawing them and wrapping the paper (Figure 2).
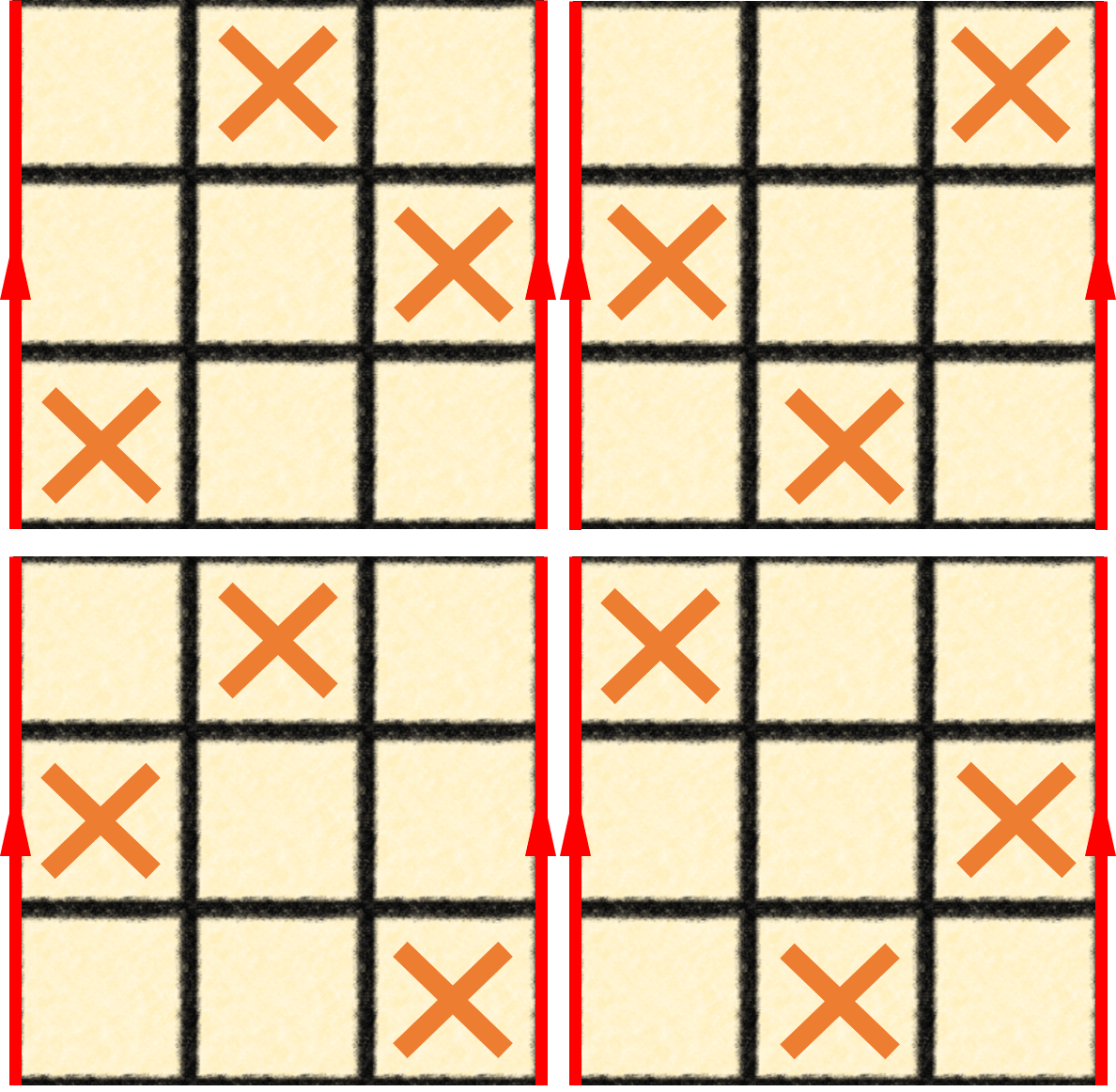
Figure 2: New win conditions created by playing tic-tac-toe on a cylindrical surface. Adapted from (Weeks, 2017).
Alternatively, the connected edges can be thought of as tiling indefinitely as shown in Figure 3 (Weeks, 2001) – which also makes the wins clear.
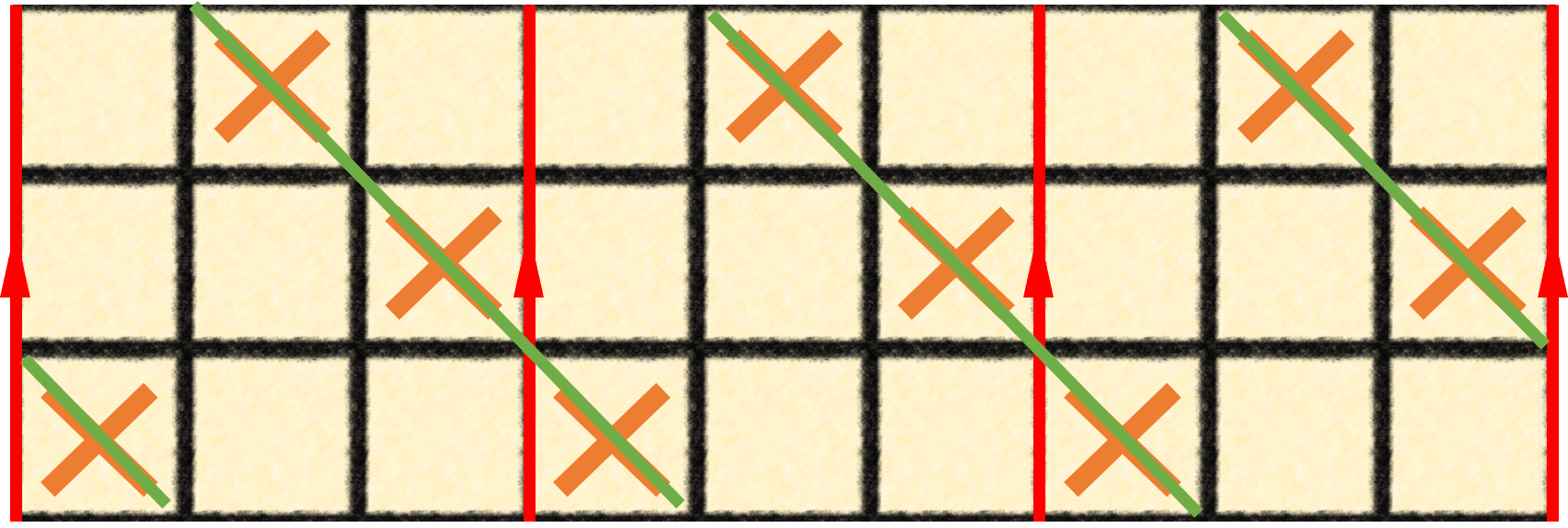
Figure 3: The cylindrical space can be tiled infinitely on either side, showing how the new win conditions form straight lines. Adapted from (Weeks, 2017).
Now, also connect the top and bottom edges at the same orientation – this would be like connecting the two ends of a flexible hose. This would create a torus, with the 3×3 board living on the surface (Kinsey, 1993). This means the board can also be tiled in the second-dimension (Figure 4). As an exercise, this can be shown to add no new win conditions and is therefore an equivalent game to the cylindrical-tic-tac-toe.
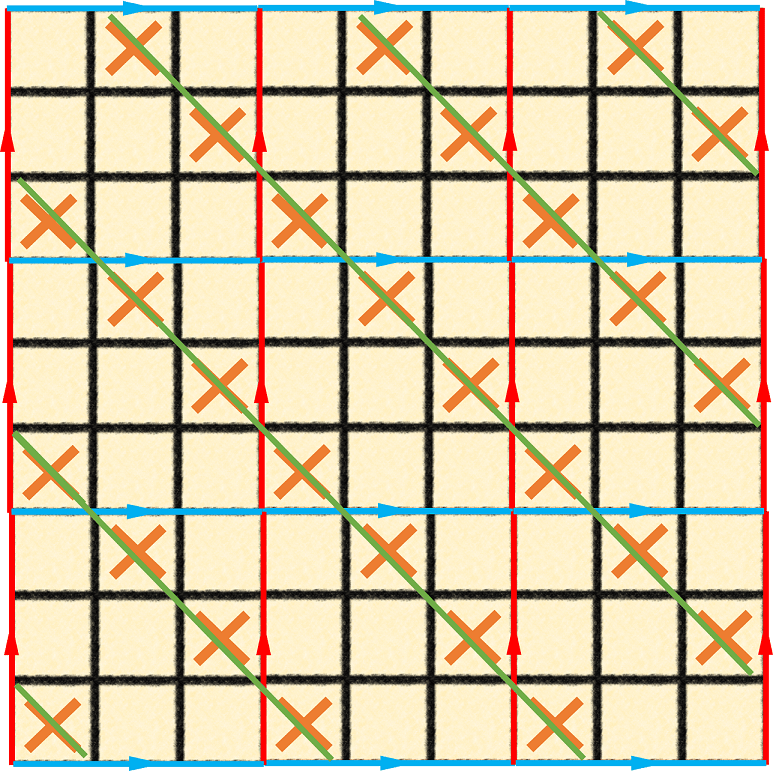
Figure 4: Tiling of tic-tac-toe on a torus world. Adapted from (Weeks, 2017).
Alternatively, the edges can be attached in opposing orientations as shown in Figure 5, thus making the board the 2-dimensional surface of a Klein bottle – a 4-dimensional shape (Gardner, 1983). Of course, more topologies can be made in 2-dimensional space, such as connecting both pairs of edges in opposing orientations, or connecting adjacent rather than opposing edges (Gardner, 1983; Kinsey, 1993).
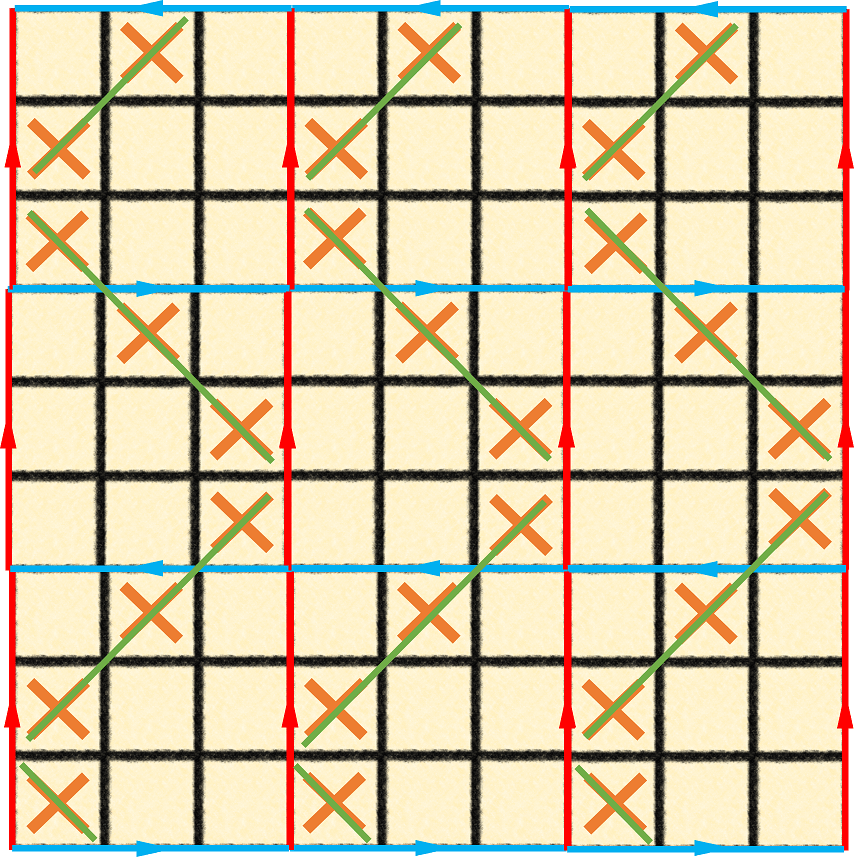
Figure 5: Tiling of tic-tac-toe on a Klein bottle world, where every other row is mirrored horizontally. Note that unlike the torus world, this does admit new win conditions, one of which is presented here. Adapted from (Weeks, 2017).
While this seems like simply a mathematical exercise, it is quite relevant in understanding our universe. Consider the torus world again, and suppose that it has an observer on a planet and one star – what would the observer see? Because all the sides are connected, the observer would not only be able to see one star, but the same star infinitely many times in each direction, shown in Figure 6. Not only that, but they would also see themselves infinitely many times (Lachièze-Rey and Luminet, 1995; Weeks, 2001). This is also possible in 3-dimensional space, and is one possibility for the shape of our universe – finite yet unbounded (Lachièze-Rey and Luminet, 1995).
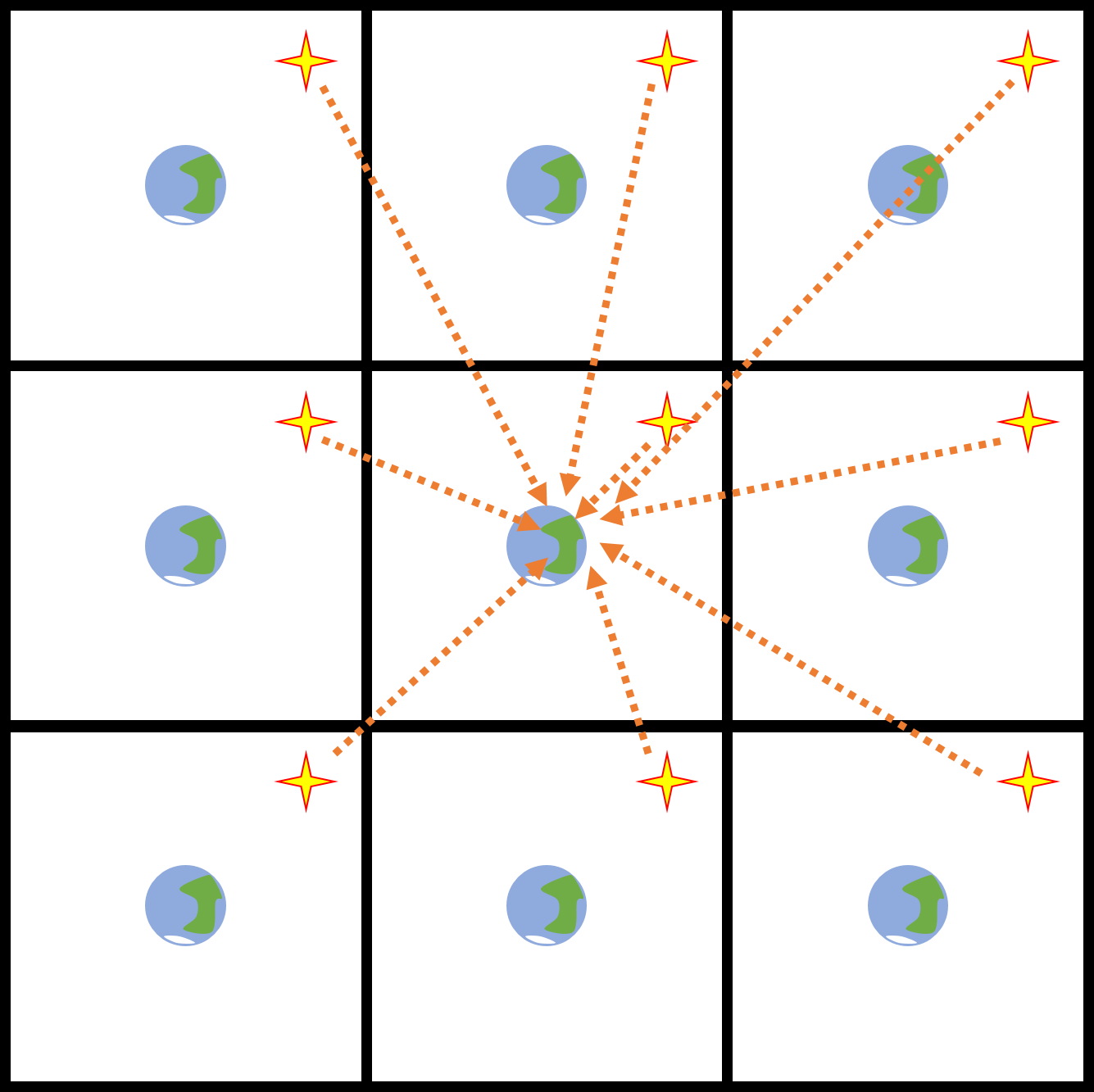
Figure 6: In a periodic universe, light from a single star can be observed from infinitely many directions. Note, however, that light still has to travel a distance. Thus, if the speed of light is finite, as it is in our universe, light coming from farther tilings will be “older”.
While this may seem unlikely, considering we cannot see ourselves in the night sky, consider that even in periodically-repeating space, the speed of light would still be finite. Thus, the repeated images would be of the past – we may be able to see our solar system as it was forming, or even before the gas had condensed. Evidence that the universe could be periodic can be seen in the cosmic microwave background. While observations best fit flat, infinite space, they are still consistent with some periodic topologies – in particular the Poincaré dodecahedral space shown in Figure 7 (Luminet, 2016). Thus, the universe may be smaller than we expect, despite seemingly covering infinite space.

Figure 7: A view of a periodic universe with Poincaré dodecahedral topology, where the “base” fundamental space is in the shape of a dodecahedron. (Weeks, 2017).
References
Gardner, M., 1983. Martin Gardner’s Sixth Book of Mathematical Diversions from Scientific American. Chicago, IL: University of Chicago Press.
Kinsey, L., 1993. Topology of surfaces. New York, NY: Springer-Verlag New York.
Lachièze-Rey, M., and Luminet, J.-P., 1995. Cosmic topology. Physics Reports, 254(3), pp.135–214.
Luminet, J.-P., 2016. The Status of Cosmic Topology after Planck Data.
Weeks, J., 2001. The shape of space. 2nd ed. Boca Raton, FL: CRC Press.
Weeks, J., 2017. Topology and Geometry Software. [online] National Science Foundation. Available at: http://www.geometrygames.org/ [Accessed 12 Feb. 2017].